Privacy laws like GDPR & CCPA require websites to obtain consent from visitors for most types of cookies and provide a detailed explanation of their purpose.
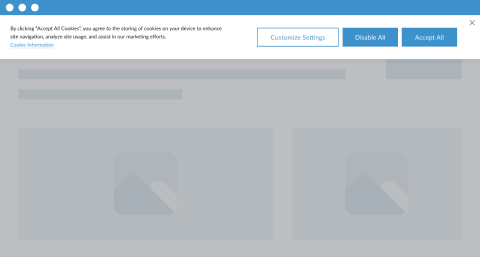
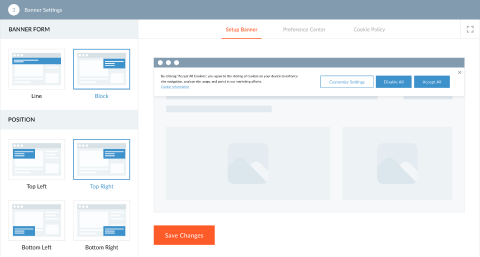
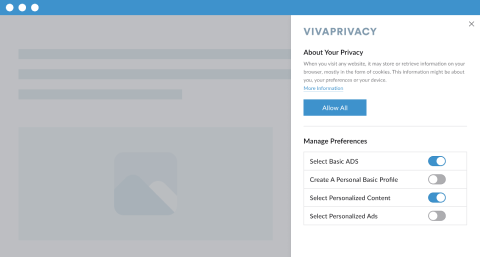
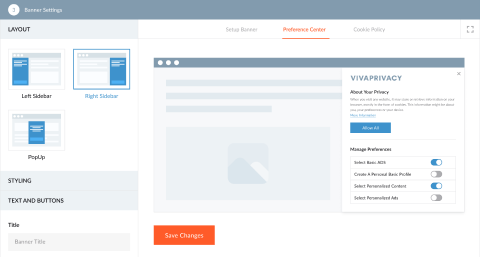
Tailor a banner based on your cookie consent approach and create a custom preference center that allows visitors to select which types of cookies and tracking technologies they want to enable or disable.
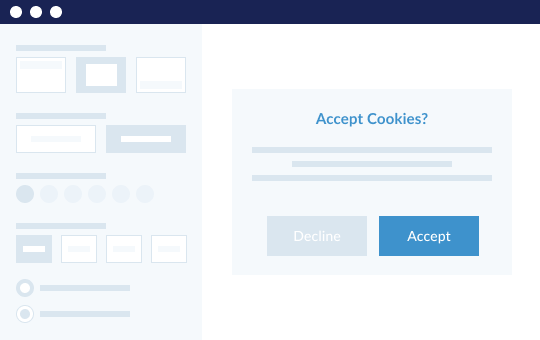
Deploy VivaPrivacy on your website with the simple addition of a script tag.
VivaPrivacy automatically scans, categorizes, and adds a description to all cookies found on your website.
Build an audit trail of detailed records of cookie consent for compliance purposes and leverage visual dashboards to verify and monitor your consent approach.
Automatically scan, find, and block selected tracking technologies on your website until the visitor has provided consent.
No limit on website visitors count.
Offer localized text with control of location and languages.
VivaPrivacy works perfectly on any device and screen size.